Мощность

Квантовая физика и элементы астрофизики

Наиболее трудна для понимания старшеклассниками квантовая физика, изучающая квантовую теорию поля, квантовую механику и математическое описание процессов. Разрабатываться это направление начало только в XX веке, благодаря работам Эйнштейна, Планка, Шредингера, Гейзенберга и других ученых. В школьной программе оно занимает не так много места, как другие разделы, поэтому количество заданий по квантовой физике несколько меньше.

Остановимся на некоторых элементах содержания, которые необходимо знать, чтобы успешно пройти испытание.

Подраздел	Элементы содержания
Корпускулярно-волновой дуализм	Гипотеза и формула Планка. Фотон, его энергия и импульс. Фотоэффект, уравнение Эйнштейна. Волны де Бройля. Дифракция электронов. Давление света.
Физика атома	Модель атома. Работы Бора. Фотоны, их поглощение и излучение. Линейчатые спектры. Лазер.
Физика атомного ядра	Массовое число и заряд ядра. Изотопы. Ядерные силы. Радиоактивность и радиоактивный распад. Гамма-излучение. Ядерные реакции.
Элементы астрофизики	Строение Солнечной системы. Характеристики звезд и наука об их происхождении. Галактики. Вселенная, ее масштабы и эволюция.

В экзаменационной работе квантовой физике и астрофизике посвящены задания №19–21 и №24 первой части. Задачи №26, 27 и 32 основаны на знании школьниками нескольких разделов: кроме квантовой физики, еще механики и электродинамики. Основные формулы, имеющие отношение к этой теме, вынесены в отдельную таблицу кодификатора.

Изучения одной теории по физике для подготовки к ЕГЭ недостаточно, нужно еще применять эти знания на практике, поэтому важную роль играет умение решать задачи. Участники должны быть способны анализировать графики и таблицы, интерпретировать результаты экспериментов, выявлять соответствия, разбираться в изменении физических величин в процессах.

Перед выпускниками школ с хорошим знанием физики и высоким баллом ЕГЭ открываются неплохие перспективы дальнейшего образования. А талантливый студент или аспирант вполне может трудоустроиться в крупную компанию и в полной мере реализовать свой потенциал.

Определения и формулы

Равномерное прямолинейное движение 

Скорость

Скоростью равномерного прямолинейного движения называют постоянную векторную величину, численно равную перемещению, которое совершает тело за единицу времени (t).

Проекция скорости на координатную ось

Перемещение

Перемещение при равномерном прямолинейном движении равно произведению скорости на время (t) этого перемещения.

Проекция перемещения на координатную ось

Равноускоренное прямолинейное движение 

Средняя скорость при неравномерном прямолинейном движении
Средняя скорость при неравномерном прямолинейном движении равна отношению перемещения на время (t), в течение которого оно совершено.

Ускорение

Ускорение тела  при его равноускоренном движении — величина, равная отношению изменения скорости к промежутку времени (t), в течение которого это изменение произошло.

Скорость

Скорость  тела в любой момент времени (t) равноускоренного прямолинейного движения определяется начальной скоростью тела и его ускорением .

Перемещение

Перемещение (s) тела в любой момент времени (t) равноускоренного прямолинейного движения определяется начальной скоростью (v0) тела и его конечной скоростью (v=v0+a×t).

Координата тела
Ускорение свободного падения

Равномерное движение по окружности 

Угловая скорость
Угловая скорость (ω) тела при равномерном движении по окружности характеризует быстроту изменения угла поворота и:

• равна отношению изменения угла поворота (Δφ) к промежутку времени (Δt), за которое это изменение произошло;
• определяется отношением линейной скорости (v) к радиусу окружности (r);
• пропорциональна частоте обращения (n);
• обратно пропорциональна периоду обращения (Т)

Частота обращения (n) —

Период обращения (Т) — время совершения телом одного полного оборота.

Линейная скорость

• пропорциональна длине окружности (2πr) и обратно пропорциональна периоду обращения (T)
• пропорциональна длине окружности (2πr) и частоте обращения (n).

Центростремительное ускорение

• пропорционально квадрату скорости (v) и обратно пропорционально радиусу окружности (r);
• связано с периодом обращения (T) и частотой обращения (n) формулами:

Механика

Кинематика

Равноускоренное движение:
Ускорение:	`a=(v-v_0)/t`
Скорость:	`v=v_0+at`
Путь, пройденный телом:	`S=v_0t+(at^2)/2`	Три варианта формулы
	`S=(v^2-v_0^2)/(2a)`
	`S=(v+v_0)/2t`
`v(t)=S'(t)`
`a(t)=v'(t)=S»(t)`

Тело брошено под углом к горизонту:
Горизонтальная проекция скорости:	`v_x=v_0*cosalpha=const`	Горизонтальная скорость постоянна
Вертикальная проекция скорости:	`v_y=v_0*sinalpha`	Вертикальная скорость меняется с ускорением `g`

Движение по окружности:
Центростремительное ускорение:	`a_(цс)=v^2/R=omega^2R`
Угловая скорость:	`omega=(Deltavarphi)/(Deltat)=(2pi)/T=2pinu`
Связь линейной и угловой скоростей:	`v=omegaR`

Динамика

Плотность:	`rho=m/V`
Второй закон Ньютона:	`vec F=mvec a`	где `vec F` — равнодействующая всех приложенных сил
Гравитационное притяжение:	`F=G(m_1m_2)/R^2`
1-я космическая скорость:	`v_I=sqrt(gR)=sqrt((GM)/R)`
2-я космическая скорость:	`v_(II)=sqrt(2)*v_I`
Закон Гука:	`F=-kx`
Сила трения:	`F_(тр)=muN`
Давление:	`p=F/S`

Статика

Момент силы:	`M=F*l`
Условие равновесия:	`{(M_1+M_2+…=0),(vec F_1+vec F_2+…=0):}`	Моменты «по часовой стрелке» берём со знаком плюс, моменты «против часовой» берём с минусом
Правило рычага:	`F_1*l_1=F_2*l_2`	это частный случай условия равновесия
Давление жидкости:	`p=rhogh`
Сила Архимеда:	`F_A=rho_жgV_т`

Импульс и энергия

Импульс:	`vec p=mvec v`
Изменение импульса:	`Deltavec p=vec FDeltat`
Работа силы:	`A=F*l*cosalpha`
Мощность:	`P=A/t`
КПД:	`eta=A_(полезная)/A_(затраченная)`
Кинетическая энергия:	`E_к=(mv^2)/2`
Потенциальная энергия тяжести:	`E_п=mgh`
Потенциальная энергия пружины:	`E_п=(kx^2)/2`

Механические колебания и волны

`x(t)=Asin(omegat+varphi_0)`
`v(t)=x'(t)=Aomegacos(omegat+varphi_0)`
`a(t)=v'(t)=-Aomega^2sin(omegat+varphi_0)`
Период колебаний:	`T=1/nu=(2pi)/omega`
Период математического маятника:	`T=2pisqrt(l/g)`
Период пружинного маятника:	`T=2pisqrt(m/k)`
Скорость волны:	`v=lambdanu`

Описание оптических структур

В приборах и устройствах допустимо использование несколько линз одновременно. Это может быть сделано для большего коэффициента увеличения или меньшего размера, который будет занимать система в целом. Тогда возникает вопрос — какой итоговой характеристикой будет обладать подобная конструкция. На этот вопрос отвечает одна из формул по физике 11 класса, отвечающая за несколько линз одновременно.

Правило гласит, что общая сила будет равна сумме всех входящих в систему оптических сил, то есть характеристика каждой линзы. В формульном выражении это выглядит так:

D= D1 + D2 +…+Dn

Здесь

D — показатель оптической силы системы в целом и каждой из линз в отдельности.

Эта формула применяется не только для микроскопов или биноклей, например. Она пригодна для анализа различных пленочных структур или кристаллических формирований.

Электростатика

Электрический заряд может быть найден по формуле:

Линейная плотность заряда:

Поверхностная плотность заряда:

Объёмная плотность заряда:

Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):

Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:

Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):

Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):

Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:

Напряженность электрического поля, которую создает заряженная плоскость:

Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

Определение потенциала задаётся выражением:

Потенциал, который создает точечный заряд или заряженная сфера:

Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):

Для диэлектрической проницаемости вещества верно следующее:

Определение электрической ёмкости задаётся формулой:

Ёмкость плоского конденсатора:

Заряд конденсатора:

Напряжённость электрического поля внутри плоского конденсатора:

Сила притяжения пластин плоского конденсатора:

Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):

Объёмная плотность энергии электрического поля:

Магнетизм

Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:

Момент сил действующих на рамку с током:

Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:

Радиус траектории полета заряженной частицы в магнитном поле:

Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:

Индукция поля в центре витка с током радиусом R:

Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:

Магнитная проницаемость вещества выражается следующим образом:

Магнитным потоком Φ через площадь S контура называют величину заданную формулой:

ЭДС индукции рассчитывается по формуле:

При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):

Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Индуктивность катушки:

Где: n — концентрация витков на единицу длины катушки:

Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:

ЭДС самоиндукции возникающая в катушке:

Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):

Объемная плотность энергии магнитного поля:

Тепловые явления

Молекулярная физика

Средняя кинетическая энергия молекул	`bar E_к=3/2kT`	Здесь и далее рассматриваем только идеальный одноатомный газ
Давление газа:	`p=nkT`
Уравнение Менделеева-Клайперона:	`pV=nuRT`
Количество вещества в молях:	`nu=m/M=N/N_A`	M — молярная масса, берём её из таблицы Менделеева, не забываем переводить в кг/моль
Внутренняя энергия:	`U=3/2nuRT`
Закон Дальтона для смеси:	`p=p_1+p_2+…`
Относительная влажность:	`varphi=p_(парц)/p_(насыщ)=rho_(парц)/rho_(насыщ)`	См. также таблицу давления и плотности насыщенного водяного пара
Уравнение теплобаланса:	`Q_1+Q_2+Q_3+…=0`	`Q>0` в процессах, где теплота выделяется, и `Q

Термодинамика

`Q=cmDeltaT`	где `с` — удельная теплоёмкость
`Q=lambdam`	где `lambda` — удельная теплота плавления
`Q=rm`	где `r` — удельная теплота парообразования
`Q=qm`	где `q` — удельная теплота сгорания

Первое начало термодинамики:	`Q=DeltaU+A`
Работа газа в любом термодинамическом процессе — это площадь под pV-графиком		`A=int_1^2pdV`(формулу запоминать не обязательно)
Работа в изобарном процессе:	`A=p*DeltaV`
Работа газа всегда связана с изменением объёма:	`Vuarr rArr A>0«Vdarr rArr A`V=const rArr A=0`
Работа внешних сил над газом:	`A_(внеш.сил)=-A_(газа)`
КПД:	`eta=A_(цикл)/Q_н=(Q_н-Q_х)/Q_н`
Машина Карно:	`eta=(T_н-T_х)/T_н`

Молекулярная физика

Химическое количество вещества находится по одной из формул:

Масса одной молекулы вещества может быть найдена по следующей формуле:

Связь массы, плотности и объёма:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Определение концентрации задаётся следующей формулой:

Для средней квадратичной скорости молекул имеется две формулы:

Средняя кинетическая энергия поступательного движения одной молекулы:

Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:

Следствия из основного уравнения МКТ:

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):

Газовые законы. Закон Бойля-Мариотта:

Закон Гей-Люссака:

Закон Шарля:

Универсальный газовый закон (Клапейрона):

Давление смеси газов (закон Дальтона):

Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

Оптика

Прохождение границы двух сред:

Закон отражения:	`alpha=gamma`
Показатель преломления:	`n=c/v`
Закон преломления:	`sinalpha/sinbeta=n_2/n_1`
	`nu_1=nu_2`
	`n_1lambda_1=n_2lambda_2`

Линзы:

Оптическая сила линзы:	`D=1/F`	где F — фокусное расстояние
Формула тонкой линзы:	`1/F=1/d+1/f`	где d — расстояние от линзы до предмета, f — от линзы до изображения
Каждое слагаемое может входить в формулу со знаком плюс или минус:`+1/F` для собирающей линзы`-1/F` для рассеивающей линзы `+1/d` для действительного предмета`-1/d` для мнимого предмета (построенного другой оптической системой)`+1/f` для действительного изображения`-1/f` для мнимого изображения
Линейное увеличение:	`Г=h/H=f/d`	где H — высота предмета, h — высота изображения

Волновая оптика:

Условие максимумов интерференции:	`Deltad=klambda,   kinZZ`
Условие минимумов интерференции:	`Deltad=(2k+1)lambda/2,   kinZZ`
Формула дифракционной решётки:	`dsinvarphi=klambda,   kinZZ`

Задания повышенного уровня сложности на 2 балла

Задания повышенной сложности оцениваются в 2 балла. Впрочем, первая часть ЕГЭ по физике проще второй, поэтому правильнее сказать, что эти задания средние по сложности. Всего в экзамене 11 задач из этой категории: 10 из первой части, 1 – из второй. В этих заданиях необходимо проанализировать ситуацию с точки зрения физика-экспериментатора.

Первая часть ЕГЭ по физике включает в себя задания трех типов:

• Выбор 2 из 5 утверждений
• Анализ изменения величин
• Установление соответствия

Рассмотрим пример каждого типа заданий.

1)   Выбор 2 из 5 утверждений.

Здесь необходимо проанализировать каждый пункт с точки зрения формул и законов физики

Важно заметить: в утверждениях никогда не встретится то, что невозможно обосновать

Выбранные варианты можно записать в любом порядке, а один балл можно получить, если выбрать одно правильное и одно неправильное утверждение.

Пример задания на выбор двух утверждений

Заметим, что пункты 1, 2, 4 связаны с температурой. Поэтому, проанализировав температуры, мы убьем сразу трех зайцев.

Запишем формулу для плотности, где M – молярная масса газа. Выразим температуру и применим ее для описания каждой точки графика.

Проанализируем полученные отношения:

• Температура 1 максимальна
• Температура 2 минимальна
• Температура 2 меньше температуры 1. Следовательно, в процессе 1-2 температура газа уменьшается. Первое утверждение верно.
• Температура 3 не является максимальной. Второе утверждение неверно.
• Отношение максимальной температуры 1 к минимальной температуре 2 равно 8. Утверждение 4 верно.

Рассмотрим утверждение 3. Из графика видим, что плотность в процессе 2-3 уменьшается. Применим формулу для массы тела:

Заметим, что масса постоянна. Так как плотность уменьшается, то объем должен увеличиваться. Утверждение 3 неверно.

Теперь проанализируем утверждение 5.

В процессе 3-1 плотность газа остается постоянной. Следовательно, объем тоже должен быть постоянным.

Работа газа зависит от увеличения или уменьшения объема. Так как объем не меняется, то работа не будет совершаться.

2) Анализ изменения величин

В этом задании описывается ситуация, затем начальные параметры меняют. Например, шарик катится с горки под действием силы тяжести, а потом массу шарика меняют. Нужно определить, как изменятся (увеличатся, уменьшатся, не изменятся) те или иные две величины.

Один балл можно получить, если вы верно определили изменение только одной величины.

Пример задания на анализ изменения величин:

Начнем со времени. Представим, что вы кидаете мячик параллельно полу с высоты колена, а потом поднимаетесь на 25 этаж своего дома и кидаете его с крыши. Будет ли он дольше лететь? Конечно, поэтому смело пишем, что время полета увеличится.

Теперь давайте разберемся с дальностью полета. Надо понимать, что эта задача – частный случай движения под углом к горизонту. Описываться эта задача будет теми же самыми уравнениями.

Важно помнить, что движение по оси OX будет постоянным. Ведь ускорение g действует только по оси OY!

Запишем уравнение для движения вдоль Ох:

Запишем уравнение для движения вдоль Ох:

Время увеличилось, скорость не изменилась. Зависимость прямо пропорциональная, поэтому путь тоже увеличится.

3) Установление соответствия

В этих заданиях необходимо установить соответствие между графиками и физическими величинами, либо между формулами и физическими величинами. Один балл можно получить при установлении одного правильного соответствия.

Пример задания на установление соответствия:

Для выполнения этого задания нужно вспомнить формулу для изменения импульса. С одной стороны, это изменение можно записать через силу и время, а с другой – через массу и изменение скорости.

Теперь вы знаете, как решать первую часть ЕГЭ по физике! Если хотите разобраться в остальных темах по физике и не только, обратите внимание на наши онлайн-курсы. Уже более 150 тысяч выпускников подготовились с нами к ЕГЭ. Кстати, у меня на курсах MAXIMUM тоже можно поучиться!

Кстати, у меня на курсах MAXIMUM тоже можно поучиться!

Кинематика

Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):

Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

Физика 8: все формулы и определения

«Физика 8: все формулы и определения» — это Справочник по физике в 8 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 4-х страницах) и МЕЛКО (формат JPG, на 1-й странице).

1 файл(ы) 4.29 MB

Физика 8 класс. Все формулы и определения МЕЛКО на одной странице

1 файл(ы) 3.66 MB

В пособии «Физика 8: все формулы и определения» представлено 23 формулы
и определения за весь курс Физики 8 класса:

Глава 1. Тепловые явления

• § 1. Тепловое движение. температура
• § 2. Внутренняя энергия
• § 3. Способы изменения внутренней энергии тела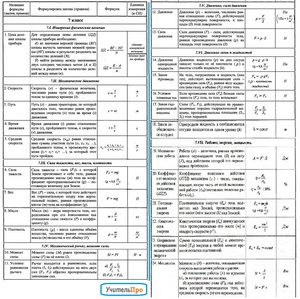
• § 4. Теплопроводность
• § 5. Конвекция
• § 6. Излучение
• § 7. Количество теплоты. Единицы количества теплоты
• § 8. Удельная теплоёмкость
• § 9. Расчёт количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении
• § 10. Энергия топлива. Удельная теплота сгорания
• § 11. Закон сохранения и превращения энергии в механических и тепловых процессах
• § 12. Агрегатные состояния вещества
• § 13. Плавление и отвердевание кристаллических тел
• § 14. График плавления и отвердевания кристаллических тел
• § 15. Удельная теплота плавления
• § 16. Испарение. Насыщенный и ненасыщенный пар
• § 17. Поглощение энергии при испарении жидкости и выделение её при конденсации пара
• § 18. Кипение
• § 19. Влажность воздуха. Способы определения влажности воздуха
• § 20. Удельная теплота парообразования и конденсации
• § 21. Работа газа и пара при расширении
• § 22. Двигатель внутреннего сгорания
• § 23. Паровая турбина
• § 24. КПД теплового двигателя

Глава 2. Электрические явления

• § 25. Электризация тел при соприкосновении. Взаимодействие заряженных тел
• § 26. Электроскоп
• § 27. Электрическое поле
• § 28. Делимость электрического заряда. Электрон
• § 29. Строение атомов
• § 30. Объяснение электрических явлении
• § 31. Проводники, полупроводники и непроводники электричества
• § 32. Электрический ток. Источники электрического тока
• § 33. Электрическая цепь и её составные части
• § 34. Электрический ток в металлах
• § 35. Действия электрического тока
• § 36. Направление электрического тока
• § 37. Сила тока. Единицы силы тока
• § 38. Амперметр. Измерение силы тока
• § 39. Электрическое напряжение
• § 40. Единицы напряжения
• § 41. Вольтметр. Измерение напряжения
• § 42. Зависимость силы тока от напряжения
• § 43. Электрическое сопротивление проводников. Единицы сопротивления
• § 44. Закон Ома для участка цепи
• § 45. Расчёт сопротивления проводника. Удельное сопротивление
• § 46. Примеры на расчет сопротивления проводника, силы тока и напряжения
• § 47. Реостаты
• § 48. Последовательное соединение проводников
• § 49. Параллельное соединение проводников
• § 50. Работа электрического тока
• § 51. Мощность электрического тока
• § 52. Единицы работы электрического тока, применяемые на практике
• § 53. Нагревание проводников электрическим током. Закон Джоуля—Ленца
• § 54. Конденсатор
• § 55. Лампа накаливания. Электрические нагревательные приборы
• § 56. Короткое замыкание. Предохранители

Глава 3. Электромагнитные явления

• § 57. Магнитное поле
• § 58. Магнитное поле прямого тока. Магнитные линии
• § 59. Магнитное поле катушки с током. Электромагниты и их применение
• § 60. Постоянные магниты. Магнитное поле постоянных магнитов
• § 61. Магнитное поле земли
• § 62. Действие магнитного поля на проводник с током. Электрический двигатель

Глава 4. Световые явления

• § 63. Источники света. Распространение света
• § 64. Видимое движение светил
• § 65. Отражение света. Закон отражения света
• § 66. Плоское зеркало
• § 67. Преломление света. Закон преломления света
• § 68. Линзы. Оптическая сила линзы
• § 69. Изображения, даваемые линзой
• § 70. Глаз и зрение

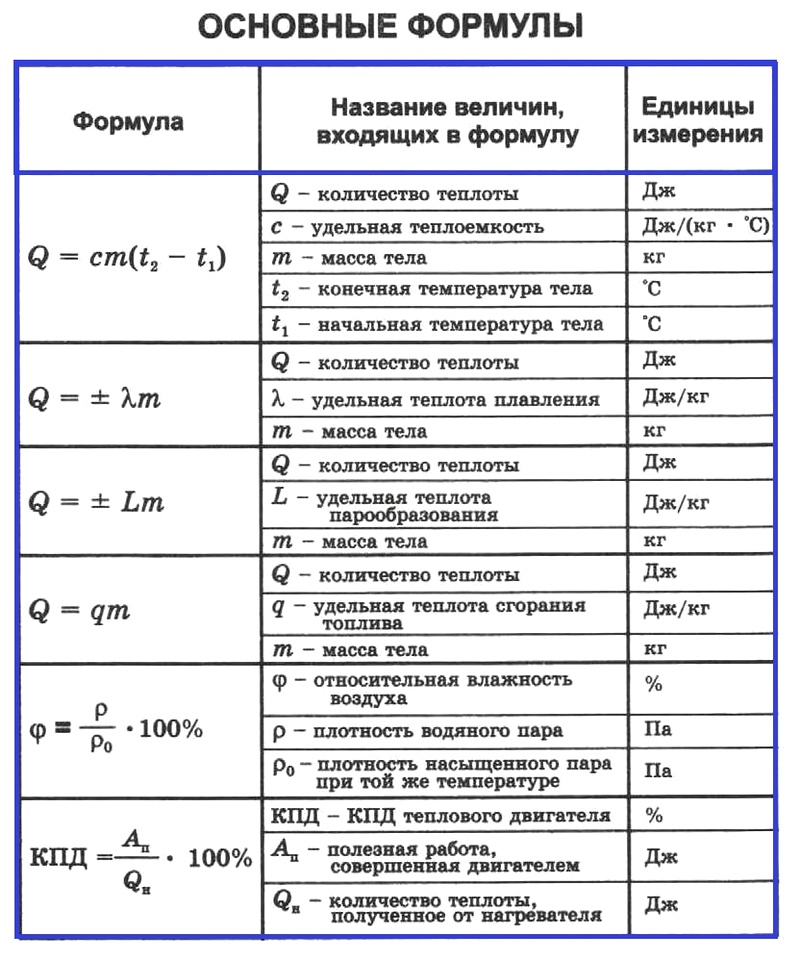
Физика 8: все формулы. Таблица 1

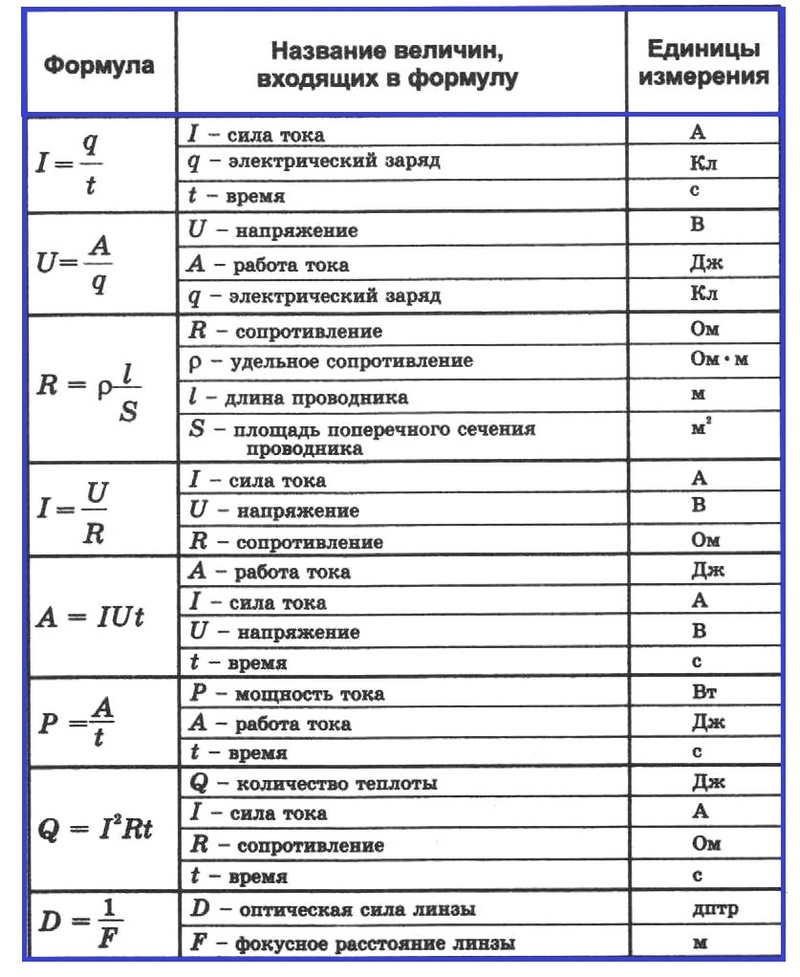
Физика 8: все формулы. Таблица 2

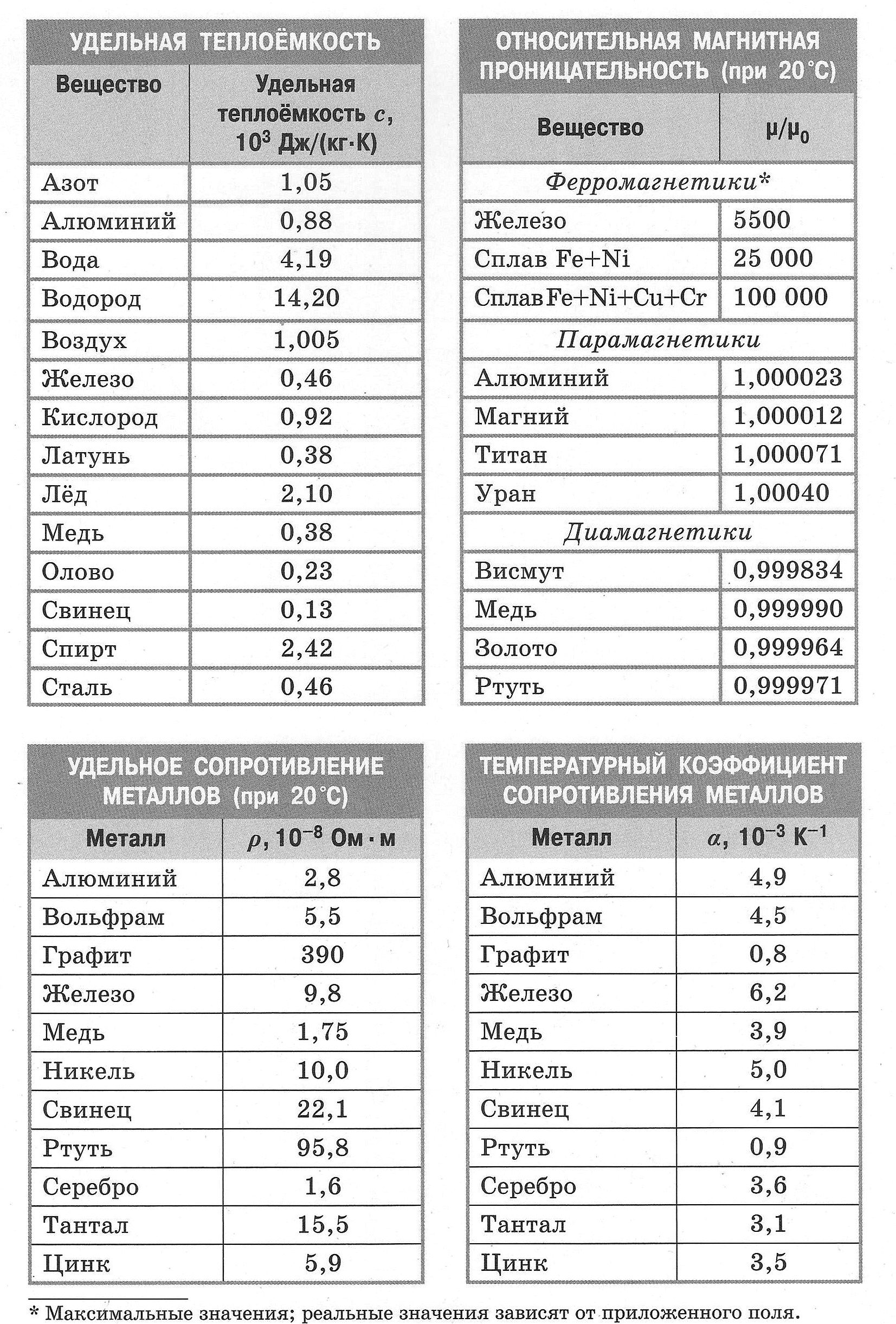
Оптика

Прохождение границы двух сред:

Закон отражения:	`alpha=gamma`
Показатель преломления:	`n=c/v`
Закон преломления:	`sinalpha/sinbeta=n_2/n_1`
	`nu_1=nu_2`
	`n_1lambda_1=n_2lambda_2`

Линзы:

Оптическая сила линзы:	`D=1/F`	где F — фокусное расстояние
Формула тонкой линзы:	`1/F=1/d+1/f`	где d — расстояние от линзы до предмета, f — от линзы до изображения
Каждое слагаемое может входить в формулу со знаком плюс или минус:`+1/F` для собирающей линзы`-1/F` для рассеивающей линзы `+1/d` для действительного предмета`-1/d` для мнимого предмета (построенного другой оптической системой)`+1/f` для действительного изображения`-1/f` для мнимого изображения
Линейное увеличение:	`Г=h/H=f/d`	где H — высота предмета, h — высота изображения

Волновая оптика:

Условие максимумов интерференции:	`Deltad=klambda,   kinZZ`
Условие минимумов интерференции:	`Deltad=(2k+1)lambda/2,   kinZZ`
Формула дифракционной решётки:	`dsinvarphi=klambda,   kinZZ`

Работа, мощность, энергия

Механическая работа рассчитывается по следующей формуле:

Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):

Мгновенная механическая мощность:

Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:

Формула для кинетической энергии:

Потенциальная энергия тела поднятого на высоту:

Потенциальная энергия растянутой (или сжатой) пружины:

Полная механическая энергия:

Связь полной механической энергии тела или системы тел и работы внешних сил:

Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):

Тепловые явления

Молекулярная физика

Средняя кинетическая энергия молекул	`bar E_к=3/2kT`	Здесь и далее рассматриваем только идеальный одноатомный газ
Давление газа:	`p=nkT`
Уравнение Менделеева-Клайперона:	`pV=nuRT`
Количество вещества в молях:	`nu=m/M=N/N_A`	M — молярная масса, берём её из таблицы Менделеева, не забываем переводить в кг/моль
Внутренняя энергия:	`U=3/2nuRT`
Закон Дальтона для смеси:	`p=p_1+p_2+…`
Относительная влажность:	`varphi=p_(парц)/p_(насыщ)=rho_(парц)/rho_(насыщ)`	См. также таблицу давления и плотности насыщенного водяного пара
Уравнение теплобаланса:	`Q_1+Q_2+Q_3+…=0`	`Q>0` в процессах, где теплота выделяется, и `Q

Термодинамика

`Q=cmDeltaT`	где `с` — удельная теплоёмкость
`Q=lambdam`	где `lambda` — удельная теплота плавления
`Q=rm`	где `r` — удельная теплота парообразования
`Q=qm`	где `q` — удельная теплота сгорания

Первое начало термодинамики:	`Q=DeltaU+A`
Работа газа в любом термодинамическом процессе — это площадь под pV-графиком		`A=int_1^2pdV`(формулу запоминать не обязательно)
Работа в изобарном процессе:	`A=p*DeltaV`
Работа газа всегда связана с изменением объёма:	`Vuarr rArr A>0«Vdarr rArr A`V=const rArr A=0`
Работа внешних сил над газом:	`A_(внеш.сил)=-A_(газа)`
КПД:	`eta=A_(цикл)/Q_н=(Q_н-Q_х)/Q_н`
Машина Карно:	`eta=(T_н-T_х)/T_н`

Значения других единиц, равные введённым выше

 открыть 

 свернуть 

Международная система (СИ)

джоуль в секунду → мегаватт (МВт)
джоуль в секунду → киловатт (кВт)

джоуль в секунду → ватт (Вт)
джоуль в секунду → вольт-ампер (В-А)

Единицы:

мегаватт
(МВт)

 /
киловатт
(кВт)

 /
ватт
(Вт)

 /
вольт-ампер
(В-А)

 открыть 

 свернуть 

СГС и внесистемные единицы

джоуль в секунду → гигакалорий в секунду
джоуль в секунду → килокалорий в секунду
джоуль в секунду → калорий в секунду
джоуль в секунду → гигакалорий в минуту
джоуль в секунду → килокалорий в минуту
джоуль в секунду → калорий в минуту
джоуль в секунду → гигакалорий в час
джоуль в секунду → килокалорий в час
джоуль в секунду → калорий в час
джоуль в секунду → котловая лошадиная сила (hp(S))

джоуль в секунду → электрическая лошадиная сила (hp(E))
джоуль в секунду → гидравлическая лошадиная сила
джоуль в секунду → механическая лошадиная сила (hp(I))
джоуль в секунду → метрическая лошадиная сила (hp(M))
джоуль в секунду → килограмм-сила метр в секунду (кгс*м/с)
джоуль в секунду → джоуль в секунду
джоуль в секунду → джоуль в минуту
джоуль в секунду → джоуль в час
джоуль в секунду → эрг в секунду
джоуль в секунду → метрическая тонна охлаждения (RT)
джоуль в секунду → фригория в час (fg/h)

Единицы:

гигакалорий в секунду

 /
килокалорий в секунду

 /
калорий в секунду

 /
гигакалорий в минуту

 /
килокалорий в минуту

 /
калорий в минуту

 /
гигакалорий в час

 /
килокалорий в час

 /
калорий в час

 /
котловая лошадиная сила
(hp(S))

 /
электрическая лошадиная сила
(hp(E))

 /
гидравлическая лошадиная сила

 /
механическая лошадиная сила
(hp(I))

 /
метрическая лошадиная сила
(hp(M))

 /
килограмм-сила метр в секунду
(кгс*м/с)

 /
джоуль в секунду

 /
джоуль в минуту

 /
джоуль в час

 /
эрг в секунду

 /
метрическая тонна охлаждения
(RT)

 /
фригория в час
(fg/h)

 открыть 

 свернуть 

Британские и американские единицы

джоуль в секунду → американская тонна охлаждения (USRT)
джоуль в секунду → британская термальная единица в секунду (BTU/s)

джоуль в секунду → британская термальная единица в минуту (BTU/min)
джоуль в секунду → британская термальная единица в час (BTU/hr)
джоуль в секунду → фут фунт-сила в секунду (ft*lbf/s)

Единицы:

американская тонна охлаждения
(USRT)

 /
британская термальная единица в секунду
(BTU/s)

 /
британская термальная единица в минуту
(BTU/min)

 /
британская термальная единица в час
(BTU/hr)

 /
фут фунт-сила в секунду
(ft*lbf/s)

 открыть 

 свернуть 

Естественнные единицы

В физике естественные единицы измерения базируются только на фундаментальных физических константах. Определение этих единиц никак не связано ни с какими историческими человеческими построениями, только с фундаментальными законами природы.

джоуль в секунду → планковская мощность (L²MT⁻³)

Единицы:

планковская мощность
(L²MT⁻³)

Основы специальной теории относительности (СТО)

Релятивистское сокращение длины:

Релятивистское удлинение времени события:

Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:

Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:

Энергия покоя тела:

Любое изменение энергии тела означает изменение массы тела и наоборот:

Полная энергия тела:

Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:

Релятивистское увеличение массы:

Кинетическая энергия тела, движущегося с релятивистской скоростью:

Между полной энергией тела, энергией покоя и импульсом существует зависимость:

Механика

Кинематика

Равноускоренное движение:
Ускорение:	`a=(v-v_0)/t`
Скорость:	`v=v_0+at`
Путь, пройденный телом:	`S=v_0t+(at^2)/2`	Три варианта формулы
	`S=(v^2-v_0^2)/(2a)`
	`S=(v+v_0)/2t`
`v(t)=S'(t)`
`a(t)=v'(t)=S»(t)`

Тело брошено под углом к горизонту:
Горизонтальная проекция скорости:	`v_x=v_0*cosalpha=const`	Горизонтальная скорость постоянна
Вертикальная проекция скорости:	`v_y=v_0*sinalpha`	Вертикальная скорость меняется с ускорением `g`

Движение по окружности:
Центростремительное ускорение:	`a_(цс)=v^2/R=omega^2R`
Угловая скорость:	`omega=(Deltavarphi)/(Deltat)=(2pi)/T=2pinu`
Связь линейной и угловой скоростей:	`v=omegaR`

Динамика

Плотность:	`rho=m/V`
Второй закон Ньютона:	`vec F=mvec a`	где `vec F` — равнодействующая всех приложенных сил
Гравитационное притяжение:	`F=G(m_1m_2)/R^2`
1-я космическая скорость:	`v_I=sqrt(gR)=sqrt((GM)/R)`
2-я космическая скорость:	`v_(II)=sqrt(2)*v_I`
Закон Гука:	`F=-kx`
Сила трения:	`F_(тр)=muN`
Давление:	`p=F/S`

Статика

Момент силы:	`M=F*l`
Условие равновесия:	`{(M_1+M_2+…=0),(vec F_1+vec F_2+…=0):}`	Моменты «по часовой стрелке» берём со знаком плюс, моменты «против часовой» берём с минусом
Правило рычага:	`F_1*l_1=F_2*l_2`	это частный случай условия равновесия
Давление жидкости:	`p=rhogh`
Сила Архимеда:	`F_A=rho_жgV_т`

Импульс и энергия

Импульс:	`vec p=mvec v`
Изменение импульса:	`Deltavec p=vec FDeltat`
Работа силы:	`A=F*l*cosalpha`
Мощность:	`P=A/t`
КПД:	`eta=A_(полезная)/A_(затраченная)`
Кинетическая энергия:	`E_к=(mv^2)/2`
Потенциальная энергия тяжести:	`E_п=mgh`
Потенциальная энергия пружины:	`E_п=(kx^2)/2`

Механические колебания и волны

`x(t)=Asin(omegat+varphi_0)`
`v(t)=x'(t)=Aomegacos(omegat+varphi_0)`
`a(t)=v'(t)=-Aomega^2sin(omegat+varphi_0)`
Период колебаний:	`T=1/nu=(2pi)/omega`
Период математического маятника:	`T=2pisqrt(l/g)`
Период пружинного маятника:	`T=2pisqrt(m/k)`
Скорость волны:	`v=lambdanu`

Электродинамика, оптика и СТО

Еще один раздел физики, по объему сопоставимый с механикой, – электродинамика. Он достаточно сложен и дается учащимся нелегко. Электродинамика изучает взаимодействие тел с электромагнитными полями, излучение и свойства тока. На экзамене одиннадцатиклассникам необходимо будет подтвердить свои знания по таким темам.

Подраздел	Элементы содержания
Электрическое поле	Электрозаряд и электрополе. Закон Кулона. Потенциальность и напряжение. Проводники, диэлектрики, конденсаторы.
Постоянный ток	Сила тока. Законы Ома для полной цепи и участка цепи. Сопротивление. Работа и мощность тока. Закон Джоуля – Ленца. Полупроводники.
Магнитное поле	Магнитная индукция. Суперпозиция магнитных полей. Силы Ампера и Лоренца. Опыт Эрстеда.
Электромагнитная индукция	Закон Фарадея. Правило Ленца. Индуктивность. Энергия магнитного поля.
Электромагнитные волны и колебания	Колебательный контур и сохранение в нем энергии. Формула Томсона. Переменный ток. Производство электроэнергии, ее производство и потребление. Свойства и использование в быту электромагнитных волн.
Оптика	Распространение, преломление и отражение света. Линзы рассеивающие и собирающие. Интерференция, дифракция и дисперсия света. Устройство фотоаппарата. Глаз.

К этому разделу примыкают и темы, посвященные основам теории относительности. Это скорость света в вакууме, открытия Эйнштейна, энергия и импульс частицы. В КИМ владение материалом по электродинамике и СТО проверяется при помощи упражнений №13–18 первой части, а также №26, 31 и 32 второй части.