Егэ по математике
Содержание:
- Электричество и магнетизм
- Независимые события
- Формулы по базовой математике для ЕГЭ
- Дробно рациональные уравнения
- Несовместные события
- Основные формулы для профильного ЕГЭ
- Теория к заданию 4 из ЕГЭ по математике (профильной)
- Противоположные события
- Независимые события
- Несовместные события
- Совместные события
- Особенности уровней ЕГЭ по математике
- Какие темы важно знать для ЕГЭ по математике 2022?
- Формулы для ОГЭ-2022 по математике
- Молекулярная физика и термодинамика
- Оптика
- Какие формулы необходимы для сдачи ЕГЭ по профильной математике?
- Тригонометрия
- Геометрия на плоскости (планиметрия)
- Обратные тригонометрические функции и простейшие тригонометрические уравнения
- Механика
- Показательные уравнения
- Геометрия в пространстве (стереометрия)
Электричество и магнетизм
Электрическое поле
| Сила Кулона: | `F=k(q_1*q_2)/r^2` |
| Поле точечного заряда: | `E=kq/r^2` | |
| Сила, действующая на заряд в эл.поле: | `F=q*E` | |
| Потенциал поля: | `varphi=W/q` | где `W` — потенциальная энергия заряда в поле |
| Работа по перемещению заряда: | `A=DeltaW=qDeltavarphi=qU` | |
| Напряжение в однородном поле: | `U=Ed` | |
| Ёмкость конденсатора (любого): | `C=q/U` | |
| Ёмкость плоского конденсатора: | `C=(epsilonepsilon_0S)/d` | |
| Параллельное соединение конденсаторов: | `C_(общ)=C_1+C_2+…` | |
| Последовательное соединение конденсаторов: | `1/C_(общ)=1/C_1+1/C_2+…` | |
| Энергия конденсатора: | `W_c=(CU^2)/2=(qU)/2=q^2/(2C)` |
Постоянный ток
| Сила тока: | `I=(Deltaq)/(Deltat)` | |
| Переменный ток: | `I(t)=q'(t)` | |
| Сопротивление: | `R=rhol/S` | где `rho` — удельное сопротивление |
| Закон Ома для участка цепи: | `I=U/R` | |
| Закон Ома для полной цепи: | `I=varepsilon/(R+r)` | |
| Параллельное соединение проводников: | `1/R=1/R_1+1/R_2+…` | |
| `R=(R_1*R_2*…)/(R_1+R_2+…)` | ||
| `I=I_1+I_2+…` | ||
| `U=U_1=U_2=…` | ||
| Последовательное соединение проводников: | `R=R_1+R_2+…` | |
| `I=I_1=I_2=…` | ||
| `U=U_1+U_2+…` | ||
| Мощность тока: | `P=UI=I^2R=U^2/R` | |
| Закон Джоуля-Ленца: | `Q=I^2Rt` |
Электромагнитная индукция:
| Магнитный поток: | `Ф=BScosalpha` |
| Закон электромагнитной индукции: | `varepsilon_i=-(DeltaФ)/(Deltat)=-Ф’_t` |
| ЗДС в движущемся проводнике: | `varepsilon_i=Blvsinalpha` |
| Индуктивность: | `L=Ф/I` |
| ЭДС самоиндукции: | `varepsilon_(si)=-L(DeltaI)/(Deltat)=-LI’_t` |
| Энергия катушки с током: | `W_L=(LI^2)/2` |
Электромагнитные колебания и волны:
| `q(t)=q_0sin(omegat+varphi_0)` |
| `I(t)=q'(t)=q_0omegacos(omegat+varphi_0)=I_0cos(omegat+varphi_0)` |
| Формула Томсона: | `T=2pisqrt(LC)` |
| `omega=(2pi)/T=1/sqrt(LC)` | |
| Скорость электромагнитной волны: | `c=lambdanu` |
Независимые события
Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:
$Р(А·В)=Р(А)·Р(В)$
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.
Решения:
Вероятность $Р(А)$ — выиграет первый билет.
Вероятность $Р(В)$ — выиграет второй билет.
События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей
$Р(А·В)=Р(А)·Р(В)$
$Р=0,15·0,12=0,018$
Ответ: $0,018$
Формулы по базовой математике для ЕГЭ
Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:
- таблица квадратных чисел от 0 до 99;
- свойства арифметического квадратного корня;
- формулы сокращенного умножения;
- корни квадратного уравнения;
- свойства степени и логарифма;
- теорема Пифагора;
- формула расчета длины окружности и площади круга;
- расчет средней линии треугольника и трапеции;
- радиус вписанной и описанной окружности правильного треугольника;
- формулы расчета площади планиметрических фигур;
- вычисление поверхностей и объемов тел;
- основные тригонометрические функции и тождества;
- график линейной функции;
- геометрический смысл производной.
Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.
Дробно рациональные уравнения
- Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
- Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые не удовлетворяют условию ОДЗ.
Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения
Несовместные события
Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)
Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:
$Р(А+В)=Р(А)+Р(В)$
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
$Р(А+В)=Р(А)+Р(В)$
$Р = 0,3+0,18=0,48$
Ответ: $0,48$
Основные формулы для профильного ЕГЭ
Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.

Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:
- правила сокращенного умножения;
- арифметическая и геометрическая прогрессии;
- основы вероятностной теории;
- свойства степеней и логарифмов;
- азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции);
- производная (правила дифференцирования, элементарнее функции и уравнение касательной);
- первообразная;
- двухмерная планиметрия;
- правила нахождения площадей геометрических фигур;
- трехмерная стереометрия.
Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:
- ЕГЭ по математике – формулы для алгебры и начал анализа
- Формулы ЕГЭ – математика, раздел геометрия
Материалы для скачивания – в формате pdf.
Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.
Теория к заданию 4 из ЕГЭ по математике (профильной)
Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов
$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.
Вероятность события — это число из отрезка $$
В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.
Решение:
Найдем количество желтых автомобилей:
$50-35=15$
Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$
Ответ:$0,3$
Противоположные события
Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}{-}$.
$Р(А)+Р{(А)}{-}=1$
Независимые события
Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:
$Р(А·В)=Р(А)·Р(В)$
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.
Решения:
Вероятность $Р(А)$ — выиграет первый билет.
Вероятность $Р(В)$ — выиграет второй билет.
События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей
$Р(А·В)=Р(А)·Р(В)$
$Р=0,15·0,12=0,018$
Ответ: $0,018$
Несовместные события
Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)
Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:
$Р(А+В)=Р(А)+Р(В)$
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
$Р(А+В)=Р(А)+Р(В)$
$Р = 0,3+0,18=0,48$
Ответ: $0,48$
Совместные события
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.
Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:
$Р(А+В)=Р(А)+Р(В)-Р(А·В)$
В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.
Решение:
Обозначим события, пусть:
$А$ = кофе закончится в первом автомате,
$В$ = кофе закончится во втором автомате.
Тогда,
$A·B =$ кофе закончится в обоих автоматах,
$A + B =$ кофе закончится хотя бы в одном автомате.
По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.
События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:
$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$
Ответ: $0,88$
Особенности уровней ЕГЭ по математике
В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.
Базовый уровень ЕГЭ по математике
Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.
Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.
В ЕГЭ по математике базового уровня 6 тематических блоков:
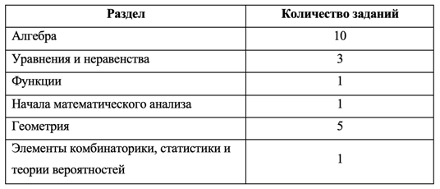
Тематические блоки, ЕГЭ по математике 2022, базовый уровень
Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.
Профильный уровень ЕГЭ по математике
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.
Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.
Какие темы важно знать для ЕГЭ по математике 2022?
В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.
Формулы тригонометрии
Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул
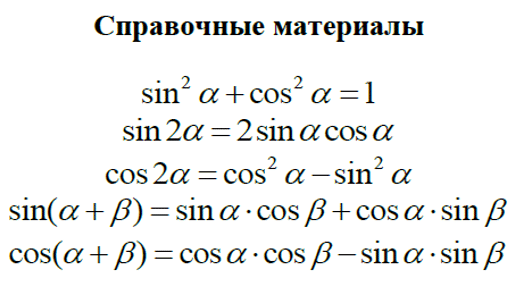
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.
Квадратные уравнения
Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.
Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.
Треугольники
Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем
Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще
Проценты
Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.
Формулы для ОГЭ-2022 по математике
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | Эти две формулы заучивать не обязательно, но желательно |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | m — число благоприятных событийn — общее число событий |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | Когда вероятность одного события (А) не зависит от другого события (B) |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | `P(B|A)` — вероятность события B при условии, что событие A наступило |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | Когда невозможно наступление обоих событий одновременно, т.е. `P(A*B)=0` |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` | Когда оба события могут наступить одновременно |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Геометрия
Планиметрия (2D)
| Тригонометрия: | `sinA=a/c` `cosA=b/c` | ||
| `text(tg)A=sinA/cosA=a/b` | |||
| Теорема косинусов: | `c^2=a^2+b^2-2ab*cosC` | ||
| Теорема синусов: | `a/sinA=b/sinB=c/sinC=2R` | где R — радиус описанной окружности | |
| Уравнение окружности: | `(x-x_0)^2+(y-y_0)^2=R^2` | где `(x_0;y_0)` — координаты центра окружности | |
| Соотношение вписанного и центрального углов: | `beta=alpha/2=(uualpha)/2` | ||
| Описанная окружность, треугольник: | `R=(abc)/(4S)` | См. также теорему синусов. Центр лежит на пересечении срединных перпендикуляров. | |
| Вписанная окружность, треугольник: | `r=S/p` | где p — полупериметр многоугольника. Центр лежит на пересечении биссектрис. | |
| Описанная окружность, четырёхугольник: | `alpha+gamma=beta+delta=180^circ` | ||
| Вписанная окружность, четырёхугольник: | `a+c=b+d` | ||
| Свойство биссектрисы: | `a/x=b/y` | ||
| Теорема о пересекающихся хордах: | `AM*BM=CM*DM` | Эти теоремы необходимо уметь выводить | |
| Теорема об угле между касательной и хордой: | `alpha=1/2uuAB` | ||
| Теорема о касательной и секущей: | `CM^2=AM*BM` | ||
| Теорема об отрезках касательных: | `AB=AC` |
Площади фигур:
Молекулярная физика и термодинамика
Молекулярная физика
| Средняя кинетическая энергия молекул | `bar E_к=3/2kT` | Здесь и далее рассматриваем только идеальный одноатомный газ |
| Давление газа: | `p=nkT` | |
| Уравнение Менделеева-Клайперона: | `pV=nuRT` | |
| Количество вещества в молях: | `nu=m/M=N/N_A` | M — молярная масса, берём её из таблицы Менделеева, не забываем переводить в кг/моль |
| Внутренняя энергия: | `U=3/2nuRT` | |
| Закон Дальтона для смеси: | `p=p_1+p_2+…` | |
| Относительная влажность: | `varphi=p_(парц)/p_(насыщ)=rho_(парц)/rho_(насыщ)` | См. также таблицу давления и плотности насыщенного водяного пара |
| Уравнение теплобаланса: | `Q_1+Q_2+Q_3+…=0` | `Q>0` в процессах, где теплота выделяется, и `Q |
Термодинамика
| `Q=cmDeltaT` | где `с` — удельная теплоёмкость |
| `Q=lambdam` | где `lambda` — удельная теплота плавления |
| `Q=rm` | где `r` — удельная теплота парообразования |
| `Q=qm` | где `q` — удельная теплота сгорания |
| Первое начало термодинамики: | `Q=DeltaU+A` | |
| Работа газа в любом термодинамическом процессе — это площадь под pV-графиком | `A=int_1^2pdV`(формулу запоминать не обязательно) | |
| Работа в изобарном процессе: | `A=p*DeltaV` | |
| Работа газа всегда связана с изменением объёма: | `Vuarr rArr A>0«Vdarr rArr A`V=const rArr A=0` | |
| Работа внешних сил над газом: | `A_(внеш.сил)=-A_(газа)` | |
| КПД: | `eta=A_(цикл)/Q_н=(Q_н-Q_х)/Q_н` | |
| Машина Карно: | `eta=(T_н-T_х)/T_н` |
Оптика
Прохождение границы двух сред:
| Закон отражения: | `alpha=gamma` | |
| Показатель преломления: | `n=c/v` | |
| Закон преломления: | `sinalpha/sinbeta=n_2/n_1` | |
| `nu_1=nu_2` | ||
| `n_1lambda_1=n_2lambda_2` |
Линзы:
| Оптическая сила линзы: | `D=1/F` | где F — фокусное расстояние |
| Формула тонкой линзы: | `1/F=1/d+1/f` | где d — расстояние от линзы до предмета, f — от линзы до изображения |
| Каждое слагаемое может входить в формулу со знаком плюс или минус:`+1/F` для собирающей линзы`-1/F` для рассеивающей линзы `+1/d` для действительного предмета`-1/d` для мнимого предмета (построенного другой оптической системой)`+1/f` для действительного изображения`-1/f` для мнимого изображения |
||
| Линейное увеличение: | `Г=h/H=f/d` | где H — высота предмета, h — высота изображения |
Волновая оптика:
| Условие максимумов интерференции: | `Deltad=klambda, kinZZ` |
| Условие минимумов интерференции: | `Deltad=(2k+1)lambda/2, kinZZ` |
| Формула дифракционной решётки: | `dsinvarphi=klambda, kinZZ` |
Какие формулы необходимы для сдачи ЕГЭ по профильной математике?
Помимо очевидного, что для сдачи профиля нужно уметь складывать, вычитать и умножать, необходимы еще некоторые знания. Все это проходится в течение школы, но повторить или заполнить пробелы перед экзаменом нужно обязательно. Вот, что пригодится:
- Формулы сокращенного умножения;
- Арифметическая и геометрическая прогрессии;
- Вероятность;
- Свойства степеней;
- Свойства логарифмов;
- Тригонометрия;
- Производные;
- Первообразные.
Список внушительный, но вполне реальный, чтобы его выучить. Для того, чтобы лишний раз не гуглить в интернете «формулы для ЕГЭ по математике профильный уровень», приложим их ниже. А начнем по порядку из списка выше.
Формулы сокращённого умножения
Первые в нашем списке – формулы сокращенного умножения – нужны для решения задания №9 из профильного уровня. Вам встретятся задачи на преобразование выражений, поэтому умение это делать будет вознаграждено баллами.
Вот то, что будет вашим спасательным кругом:
Есть те, которые знать не обязательно. Но чем большими знаниями вы будете обладать, тем легче вам будет на экзамене. Вот они:
Умея применять эти формулы для ЕГЭ по математике, профильный уровень вам уже будет решить легче. Но это далеко не все, что нужно знать, чтобы получить сто баллов за ЕГЭ.
Арифметическая и геометрическая прогрессии
Для задания №19 нужно знание арифметической и геометрической прогрессии. Прикладываем формулы для ЕГЭ по математике, профильный уровень которой невозможен без их знания:
Вероятность
Вероятность встречается в задании №4, а ведь в самом начале обычно ставят легкие задания. Тем не менее, придется применять знания, которые представлены ниже:
Перейдем к свойствам степеней, ведь в них тоже есть, что запомнить.
Свойства степеней
Эти свойства нужно знать и для того, чтобы решить «базу», так что гуманитарии тоже могут обратить внимание на это:
Как вы видите, запоминать не очень много, зато формулы не самые простые. Но есть еще сложнее, и сейчас узнаем, какие они.
Формулы логарифмов лучше всего начать с их определения:
Теперь перейдем к более сложному:
Тригонометрия
Тригонометрические уравнения встречаются в задании №13. Для того, чтобы заработать баллы, нужно знать это:
Но это еще не все. Есть такая вещь, как основное тригонометрическое тождество. Вот оно:
Формулы двойного угла:
Формулы суммы и разности аргументов:
Преобразование суммы и разности в произведение:
Формулы половинного аргумента:
На этом с тригонометрией все.
Производные
Начнем с основных правил дифференцирования:
Уравнение касательной:
Производные элементарных функций:
Закончим эту статью первообразными.
Тригонометрия
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Синус двойного угла:
Косинус двойного угла:

Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:
Тангенс разности:
Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Формулы приведения задаются в виде таблицы:

Геометрия на плоскости (планиметрия)
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:

Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Обратные тригонометрические функции и простейшие тригонометрические уравнения
Арккосинус
Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $$, косинус которого равен $а$.
Если, $|а|≤1$, то $arccos а = t ⇔ \{\table \cos (t)=a; \0≤t≤π;$
$arcos(-a) = π-arccosa$, где $0≤а≤1$
Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение
$t=±arccos a+2πk; k∈Z$
Частные случаи
$cos t =1, t = 2πk;k∈Z$
$cos t = 0, t = {π}/{2}+πk;k∈Z$
$cos t = -1, t=π+2πk;k∈Z$
Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$
$сos{2πx}/{3}=-{√3}/{2}$
${2πx}/{3}=±arccos(-{√3}/{2})+2πk;kϵZ$
${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$
${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$
${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$
Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$
$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$
$x=±1,25+3k$
Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения
$k=0$
$x_1= -1,25$
$x_2=1,25$
$к=1$
$х_1=3-1,25=1,75$
$х_2=3+1,25=4,25$
Нам подходит $1,25$ – это и есть результат
Ответ: $1,25$
Арксинус
Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.
Если, $|а|≤1$, то $arcsin a = t ⇔ \{\table \sint=a; \-{π}/{2}≤t≤{π}/{2};$
$arcsin(-a)= — arcsin a$, где $0≤а≤1$
Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:
$1. t_1 = arcsin a+2πk;k∈Z$
$t_2 = (π- arcsin a)+ 2πk;k∈Z$
$2. t=(-1)^n arcsin a+πn; n∈Z$
$3.$ Частные случаи
$sin t = 0, t=πk;k∈Z$
$sin t = 1, t={π}/{2}+2πk;k∈Z$
$sin t = -1,t=-{π}/{2}+2πk;k∈Z$
Арктангенс
$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.
$arctg a = t ⇔ \{\table \tgt=a; \-{π}/{2}≤t≤{π}/{2};$
$arctg(-a)= — arctg a$
Механика
Кинематика
| Равноускоренное движение: | ||
| Ускорение: | `a=(v-v_0)/t` | |
| Скорость: | `v=v_0+at` | |
| Путь, пройденный телом: | `S=v_0t+(at^2)/2` | Три варианта формулы |
| `S=(v^2-v_0^2)/(2a)` | ||
| `S=(v+v_0)/2t` | ||
| `v(t)=S'(t)` | ||
| `a(t)=v'(t)=S»(t)` |
| Тело брошено под углом к горизонту: | ||
| Горизонтальная проекция скорости: | `v_x=v_0*cosalpha=const` | Горизонтальная скорость постоянна |
| Вертикальная проекция скорости: | `v_y=v_0*sinalpha` | Вертикальная скорость меняется с ускорением `g` |
| Движение по окружности: | |
| Центростремительное ускорение: | `a_(цс)=v^2/R=omega^2R` |
| Угловая скорость: | `omega=(Deltavarphi)/(Deltat)=(2pi)/T=2pinu` |
| Связь линейной и угловой скоростей: | `v=omegaR` |
Динамика
| Плотность: | `rho=m/V` | |
| Второй закон Ньютона: | `vec F=mvec a` | где `vec F` — равнодействующая всех приложенных сил |
| Гравитационное притяжение: | `F=G(m_1m_2)/R^2` | |
| 1-я космическая скорость: | `v_I=sqrt(gR)=sqrt((GM)/R)` | |
| 2-я космическая скорость: | `v_(II)=sqrt(2)*v_I` | |
| Закон Гука: | `F=-kx` | |
| Сила трения: | `F_(тр)=muN` | |
| Давление: | `p=F/S` |
Статика
| Момент силы: | `M=F*l` | |
| Условие равновесия: | `{(M_1+M_2+…=0),(vec F_1+vec F_2+…=0):}` | Моменты «по часовой стрелке» берём со знаком плюс, моменты «против часовой» берём с минусом |
| Правило рычага: | `F_1*l_1=F_2*l_2` | это частный случай условия равновесия |
| Давление жидкости: | `p=rhogh` | |
| Сила Архимеда: | `F_A=rho_жgV_т` |
Импульс и энергия
| Импульс: | `vec p=mvec v` |
| Изменение импульса: | `Deltavec p=vec FDeltat` |
| Работа силы: | `A=F*l*cosalpha` |
| Мощность: | `P=A/t` |
| КПД: | `eta=A_(полезная)/A_(затраченная)` |
| Кинетическая энергия: | `E_к=(mv^2)/2` |
| Потенциальная энергия тяжести: | `E_п=mgh` |
| Потенциальная энергия пружины: | `E_п=(kx^2)/2` |
Механические колебания и волны
| `x(t)=Asin(omegat+varphi_0)` | |
| `v(t)=x'(t)=Aomegacos(omegat+varphi_0)` | |
| `a(t)=v'(t)=-Aomega^2sin(omegat+varphi_0)` | |
| Период колебаний: | `T=1/nu=(2pi)/omega` |
| Период математического маятника: | `T=2pisqrt(l/g)` |
| Период пружинного маятника: | `T=2pisqrt(m/k)` |
| Скорость волны: | `v=lambdanu` |
Показательные уравнения
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
$a^x=b$
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n·a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n∙m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
$a^{-n}={1}/{a^n}$
${a^{-n}}/{b^{-k}}={b^k}/{a^n}$
8. Радикал (корень) можно представить в виде степени с дробным показателем
$√^n{a^k}=a^{{k}/{n}}$
Виды показательных уравнений:
1. Простые показательные уравнения:
а) Вида $a^{f(x)}=a^{g(x)}$, где $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.
$f(x)=g(x)$
b) Уравнение вида $a^{f(x)}=b, b>0$
Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается
$log_{a}a^{f(x)}=log_{a}b$
$f(x)=log_{a}b$
2. Метод уравнивания оснований.
3. Метод разложения на множители и замены переменной.
- Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
- Сделать замену переменной $a^{f(x)}=t, t > 0$.
- Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
- Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Пример:
Решите уравнение $2^{3x}-7·2^{2x-1}+7·2^{x-1}-1=0$
Решение:
По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.
$(2^x)^3-{7·(2^x)^2}/{2}+{7·2^x}/{2-1}=0$
Сделаем замену переменной $2^x=t; t>0$
Получаем кубическое уравнение вида
$t^3-{7·t^2}/{2}+{7·t}/{2}-1=0$
Умножим все уравнение на $2$, чтобы избавиться от знаменателей
$2t^3-7·t^2+7·t-2=0$
Разложим левую часть уравнения методом группировки
$(2t^3-2)-(7·t^2-7·t)=0$
Вынесем из первой скобки общий множитель $2$, из второй $7t$
$2(t^3-1)-7t(t-1)=0$
Дополнительно в первой скобке видим формулу разность кубов
$2(t-1)(t^2+t+1)-7t(t-1)=0$
Далее скобку $(t-1)$ как общий множитель вынесем вперед
$(t-1)(2t^2+2t+2-7t)=0$
Произведение равно нулю, когда хотя бы один из множителей равен нулю
1) $(t-1)=0;$ 2) $2t^2+2t+2-7t=0$
Решим первое уравнение
$t_1=1$
Решим второе уравнение через дискриминант
$2t^2-5t+2=0$
$D=25-4·2·2=9=3^2$
$t_2={5-3}/{4}={1}/{2}$
$t_3={5+3}/{4}=2$
Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения
$2^x=1; 2^x={1}/{2}; 2^x=2$
$2^x=2^0; 2^x=2^{-1}; 2^x=2^1$
$х_1=0; х_2=-1; х_3=1$
Ответ: $-1; 0; 1$
4. Метод преобразования в квадратное уравнение
- Имеем уравнение вида $А·a^{2f(x)}+В·a^{f(x)}+С=0$, где $А, В$ и $С$ — коэффициенты.
- Делаем замену $a^{f(x)}=t, t > 0$.
- Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
- Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Способы разложения на множители:
Вынесение общего множителя за скобки.
Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:
- Определить общий множитель.
- Разделить на него данный многочлен.
- Записать произведение общего множителя и полученного частного (заключив это частное в скобки).
Пример:
Разложить на множители многочлен: $10a^{3}b-8a^{2}b^2+2a$.
Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:
$10a^{3}b-8a^{2}b^2+2а=2a({10a^{3}b}/{2a}-{8a^{2}b^2}/{2a}+{2a}/{2a})=2a(5a^{2}b-4ab^2+1)$
Это и есть конечный результат разложения на множители.
Геометрия в пространстве (стереометрия)
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):