Задачи с физическим смыслом

Подготовка к олимпиадам: младшие школьники (5–7 классы)

Две основные олимпиады для младших школьников — это Математический праздник и Турнир Архимеда. Наряду с ними готовимся к олимпиадам «Ломоносов», «Покори Воробьёвы горы!», «Высшая проба», «Курчатов», а также к школьному и муниципальному этапам Всероссийской олимпиады школьников по математике.

Группировка листков по темам во многом следует тематическому каталогу problems.ru (как наиболее удачному с моей точки зрения). Листки содержат:

• все задачи Матпраздника с момента его появления (то есть с 1990 года);
• все задачи Городской устной математической олимпиады для 6–7 классов с момента её появления (с 2002 года);
• все задачи Турнира Архимеда с 2011 года;
• задачи последних олимпиад «Покори Воробьёвы горы!», «Ломоносов», «Высшая проба» «Курчатов» и «Физтех», а также школьных и муниципальных этапов Всероссийской олимпиады школьников.

На базе этих листков создано пособие Олимпиадная математика. Задачник 6–7.

Бесплатно

ЕГЭ.рф

Сайт: https://егэ.рф

Платформа бесплатного тестирования уровня подготовки школьников к ЕГЭ по математике базового и профильного уровней — на основе реальных заданий от ФИПИ 2021.

Первая часть экзамена будет проверена сразу после сдачи и ты увидишь свои результаты незамедлительно. Также ты сможешь получить детальный разбор ошибок в письменных заданиях от экспертов ЕГЭ.

А по итогу ты сможешь сопоставить свои результаты с проходными баллами в ВУЗы и выбрать, куда поступать.

«4ЕГЭ»

Сайт: https://4ege.ru

Каждый видеоурок состоит из двух основных частей: простое изложение самой важной и необходимой теории по заданной теме и решения основных задач ЕГЭ

«Синергия»

Сайт: https://synergy.ru

Для вашего удобства на сайте собрано все, что может потребоваться для подготовки к экзамену по математике:

• Демоверсии и КИМы, ЕГЭ предыдущих периодов
• Теория и практика по каждому типу задания
• Официальная информация и новости

Весь теоретический материал по математике разделен на вопросы из ЕГЭ и собран в файлы. Просто выбирайте интересующую тему (вопрос, раздел), открывайте лист и повторяйте (или учите, если забыли).

Информация изложена кратко, но просто и понятно. Схематическая подача поможет все быстро запомнить.

В практическом разделе собраны готовые решения самых сложных тестов. Просто выбирайте задание и смотрите подробный план решений задач того или иного типа.

Для удобства разбора листы разделены на 2 части. В первой — только сами задачи, которые можно решать самостоятельно. Во второй части — те же задачи, но с расписанным решением.

«РешуЕГЭ»

Сайт: https://mathb-ege.sdamgia.ru

Здесь регулярно выкладывают тренировочные варианты ЕГЭ по математике базового и профильного уровней. Каждый месяц — новый вариант. По окончании тестирования система проверит ваши ответы, покажет правильные решения и выставит оценку.

Чтобы тренироваться по определённым темам, вы можете составить свой вариант — по конкретным разделам задачного каталога.

Также на сайт размещен курс из 100 занятий «Д. Д. Гущин. Готовимся к ЕГЭ по профильной математике«. В нем рассмотрены все экзаменационные темы, дано большое количество заданий из школьной математики, материалов ЕГЭ, математических олимпиад и вузовских вступительных испытаний.

Занятия включают в себя конспекты, видеоуроки с разбором простых и сложных случаев, упражнения для мгновенной самопроверки и варианты для самостоятельной работы.

Для начала нужно авторизоваться на сайте и пройти входное тестирование, чтобы был построен ваш индивидуальный образовательный маршрут.

«Математика ЕГЭ 100БАЛЛОВ»

Сайт: https://vk.com

Страница для самоподготовки к ЕГЭ по математике волонтерского некоммерческого проекта. Ежедневно размещаются различные задания и полезные материалы для подготовки к экзамену по математике.

Есть теория в картинках, видеоуроки по отдельным темам, практические задания и пробные варианты ЕГЭ.

«Математикс»

Сайт: https://www.youtube.com

Канал создан в помощь тем, кто готовится к ЕГЭ по математике.

Здесь вы найдете плейлисты, посвященные следующим темам:

• Уравнениям и Неравенствам №13 и №15 ЕГЭ
• Задачам ЕГЭ №17 №18 №19
• Стереометрии и Планиметрии №14 и №16 ЕГЭ
• Высшей Математике (Теория с примерами)
• Разборам задач из вариантов Ларина
• Разборам вариантов СтатГрад

«ЕГЭ и ОГЭ на 80-ballov. Годограф»

Сайт: https://www.youtube.com

На ютуб-канале выложены короткие видеоуроки по основным темам подготовки «ЕГЭ по Математике 2021 80 баллов». Всего в плейлисте 261 видео. Для бесплатного просмотра открыто примерно 20% полного курса.

Полный курс, включающий в себя не только видеоматериал, доступен по платной подписке на сайте проекта 80-ballov.ru. Можно сначала оценить качество материала и подачи и, при необходимости, оплатить полный доступ.

Канал Бориса Трушина

Сайт: https://www.youtube.com

Личный канал преподавателя математики онлайн-школы «Фоксфорд».

Здесь вы найдете короткие и ёмкие видеоуроки по следующим темам:

• Задания 1-12. ЕГЭ. Математика. Профильный уровень
• Задания 13-19. ЕГЭ. Математика. Профильный уровень
• Разборы вариантов ЕГЭ
• Подборки по темам: Квадратный трёхчлен, Планиметрия, Неравенства, Теория вероятностей, Тригонометрия, Теория чисел и др.

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

«Хоксвард»

Сайт: https://www.hoxward.ruТелефон: +7 499 992 2510Стоимость: пробный урок — бесплатно, от 2490 р./мес.

На курсе подготовки к ЕГЭ по математике дается вся необходимая информацию и материалы, чтобы сдать экзамен на высокий балл. Преподаватель интересно объясняет свой предмет и постоянно работает с учениками. Он и сам сдал ЕГЭ на 98 баллов, поэтому точно знает, что к чему.

Два формата подготовки:

«Курс на Сотку ЕГЭ»

• 12-16 занятий каждый месяц, ~140 р./час
• Онлайн-занятия в группе до 30 человек
• Домашняя работа + проверка
• Связь с преподавателем 24/7
• Наставник, который следит за ходом обучения и помогает по любым вопросам

Результат: знание всего материала и умение решать типовые задачи ЕГЭ.

«Курс на Сотку PRO»

• 12-16 занятий каждый месяц, ~225 р./час
• Включает в себя все то же, что и обычный курс на сотку
• Личный куратор, который помогает закрывать пробелы и сопровождает на протяжении всей подготовки

Результат: более углубленное знание всего материала и умение решать типовые задачи ЕГЭ.

SkySmart

Сайт: https://skysmart.ru/Стоимость: от 990 р. за индивидуальный урок, первый пробный урок — бесплатно

Подготовка к ОГЭ и ЕГЭ по математикеИндивидуально онлайн с сильным преподава­телем

Приведут к цели каждого ученика и помогут показать на экзамене свой максимум — и даже больше:

• Определят уровень
  Сколько баллов можно набрать уже сейчас и какого результата реально достичь
• Покажут, где теряются баллы
  Какие задания будут на экзамене и где чаще всего делают ошибки
• Подготовят без паники
  Разберете все трудные темы и научитесь справляться со стрессом

Курс разработан по методи­ческим рекомен­дациям ФИПИ в 2020 году.

1. Вычисления
   Как решать уравнения и неравенства с процентами, модулями, степенями и логарифмами.
   Задания: 1, 9, 17, 19, 5, 10, 11, 13, 19
2. Анализ функций
   Как строить графики функций, определять их производные и первообразные.
   Задания: 2, 7, 12, 18
3. Геометрия
   Как правильно читать и строить чертежи и помнить все определения и теоремы.
   Задания: 3, 6, 8, 14, 16
4. Оформление
   Как правильно перенести ответы из черновика в чистовик и как это влияет на оценку

Профессиональные преподаватели математики с сертификатами DELTA, TESOL, CELTA, ФИПИ. Каждый год сами сдают ОГЭ и ЕГЭ, чтобы быть в курсе всех изменений.

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Метод группировки

Методом группировки удобно пользоваться, когда на множители необходимо разложить многочлен с четным количеством слагаемых. В данном способе необходимо собрать слагаемые по группам и вынести из каждой группы общий множитель за скобку. У нескольких групп после вынесения в скобках должны получиться одинаковые выражения, далее эту скобку как общий множитель выносим вперед и умножаем на скобку полученного частного.

Пример:

Разложить многочлен на множители $2a^3-a^2+4a-2$

Решение:

Для разложения данного многочлена применим метод группировки слагаемых, для этого сгруппируем первые два и последние два слагаемых, при этом важно правильно поставить знак перед второй группировкой, мы поставим знак + и поэтому в скобках запишем слагаемые со своими знаками. $2a^3-a^2+4a-2=(2a^3-a^2)+(4a-2)$

$2a^3-a^2+4a-2=(2a^3-a^2)+(4a-2)$

Далее из каждой группы вынесем общий множитель

$(2a^3-a^2)+(4a-2)=a^2(2a-1)+2(2a-1)$

После вынесения общих множителей получили пару одинаковых скобок. Теперь данную скобку выносим как общий множитель.

$a^2(2a-1)+2(2a-1)=(2a-1)(a^2+2)$

Произведение данных скобок — это конечный результат разложения на множители.

Как подготовиться к ЕГЭ по математике базового уровня

В ЕГЭ по математике базового уровня 20 заданий. Они не требуют развернутой записи решения, достаточно найти ответ и правильно записать его в графу.

Один верный ответ — 1 балл.  

На выполнение заданий даётся 3 часа. Этого достаточно, чтобы всё решить, перепроверить и аккуратно перенести на чистовик.

При выполнении заданий нужно правильно понять, что именно спрашивают, а это не всегда очевидно

Для решения задачи часто нужно составить уравнение, а для этого важно не упустить ни одного элемента условия и правильно записать его математическим языком

В некоторых заданиях быстрее и проще не проводить долгих вычислений, а прикинуть или догадаться, каков верный ответ. Но после этого, разумеется, надо выполнить проверку. Так вы экономите время и развиваете математическое мышление и эрудицию.

Например, задание №16, текстовая задача.

‍Для начала мы вводим неизвестное: х деталей в час делает второй рабочий. Тогда х+4 детали в час делает первый рабочий. Известно, что 140 деталей первый рабочий делает на 4 часа быстрее, чем второй. Составляем уравнение:

‍Решаем и получаем выражение х(x+4)=140. Внимательно присмотритесь к этому равенству. Вам необходимо найти такое значение х, при котором произведение двух чисел, отличающихся на 4, будет равно 140. Необязательно считать, можно просто увидеть, что это 10 и 14. Ответ на задачу: х=10.

Чтобы развить в себе подобное математическое видение, достаточно при подготовке к ЕГЭ по математике решать как можно больше задач и не обращаться к калькулятору сразу же, как только надо что-то посчитать.

Ещё один пример. Задание №6, арифметика в жизни.

‍Здесь тоже гораздо быстрее не делить с остатком, а прикинуть, сколько автобусов может понадобиться, а затем выполнить простую операцию умножения.

В данном случае нам надо перевести 274 человека, а в автобус влезает 46. Возьмём для начала цифру 6 и умножим на 46, получилось 276 человек. Это значит, что мы нашли правильный ответ, не углубляясь в сложные расчёты.

Помните о том, что большинство задач можно решить не одним, а несколькими способами. Это поможет вам избежать ошибок, в том числе связанных с выполнением вычислений или обычной невнимательностью. Если вы решили задачу двумя способами и получили один и тот же ответ, значит, он точно правильный. При этом выбирайте более простые пути решения, а вот громоздких решений, наоборот, избегайте. Чем проще решение, тем меньше вероятность ошибиться.

Examer

Сайт — examer.ru/ege_po_matematike/2021/ Длительность обучения — индивидуально. Стоимость обучения — бесплатно для самостоятельной подготовки или 2 490 рублей в режиме Турбо с видеоуроками и разбором домашних заданий.

На этом ресурсе школьники могут готовиться только к экзамену профильного уровня. На Examer нет репетиторов или уроков как таковых. Здесь есть теория для самостоятельного изучения и задания для практической отработки. Можно заниматься дома, а можно — в любом удобном месте, поскольку у ресурса есть мобильные приложения для Android и iOS.

Существенный недостаток — отсутствие разборов заданий. Если у ребенка не получается решить какую-то задачу, с проблемой он будет разбираться самостоятельно. Для этого можно почитать теоретические материалы или воспользоваться поиском в интернете. Безусловный плюс ресурса — бесплатный доступ на неограниченной время. Это прекрасная возможность для ребят из малообеспеченных семей подтянуть свои знания по математике и подготовиться к ЕГЭ.

Перед началом обучения система попросит пройти тест на определение начального уровня знаний и предполагаемого результата ЕГЭ по математике. Затем для каждого в автоматическом режиме составляется индивидуальный план подготовки. Студент проходит модули последовательно. Каждый новый урок будет открыт после успешного решения задач по предыдущему.

Важно!
В бесплатном режиме возможности системы ограничены. Максимальную эффективность дает Турбокурс, в котором предусмотрено 12 видеоуроков в месяц

Домашние задания с проверкой преподавателя, тестирование, помощь в решении трудных задач.

Какие темы важно знать для ЕГЭ по математике 2022?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул

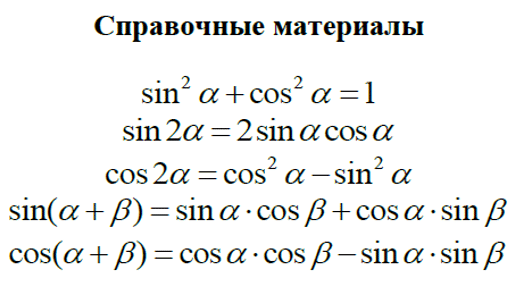
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем

Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

Принцип 3 «Много практики»

Вопрос с закреплением новых знаний на практике стоит в школе очень остро. Сложные задачи с развернутыми решением, как правило, требуют много времени. Если класс не профильный, то качественно проработать большой объем материала «от и до» за занятие практически нереально. На мой взгляд, неплохой выход из этой ситуации состоит в том, что мы математически грамотно и аккуратно расписываем образец выполнения одного прототипа задания, а затем, уже более бегло, прогоняем метод на 5-10 аналогичных примерах.

Такой подход, кроме экономии времени, позволяет ученикам сконцентрировать все внимание на методе решения и особенностях данного задания, не отвлекаясь на уже знакомые и отработанные действия. Количество заданий, прорешенных за урок, существенно увеличивается

После такой интенсивной работы ученики «привыкают» к данному типу задач, страх перед ними, как перед чем-то новым и неизвестным пропадает.

InternetUrok

Курсы подготовки к ЕГЭ по математике двух направлений: 

Базовая математика

• Количество занятий: 49
• Длительность курса: ~200 часов
• Видеоконсультации с репетитором: 1 раз в неделю (на тарифе «Репетитор онлайн»)

Основная цель  — научить пониманию математики и применению этого понимания на практике, а не просто решать задачи из банка заданий и ЕГЭ прошлых лет.

Подробно рассмотрим темы, которые входят в программу ЕГЭ базового уровня, восполним пробелы в знаниях

Обратите внимание, что в курсе нет тем и заданий, которые не предусмотрены в базовом уровне ЕГЭ по математике

Профильная математика

• Количество занятий: 60
• Длительность курса: ~240 часов
• Видеоконсультации с репетитором: 1 раз в неделю (на тарифе «Репетитор онлайн»)

Цель курса – вооружить вас знаниями, помочь сформировать навыки и отработать их на практике, что в конечном итоге позволит успешно сдать ЕГЭ.

Вы можете начать заниматься независимо от текущего уровня подготовки. Занятия можно проходить в любое удобное время и в комфортном темпе. Чтобы вы не сомневались в том, что успешно усвоили тему, каждое занятие оценивается в баллах.

Для тренировки и закрепления полученных знаний и навыков есть специальные тренажеры, в которых использованы задачи ЕГЭ прошлых лет.

Теория к заданию 4 из ЕГЭ по математике (профильной)

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}{-}$.

$Р(А)+Р{(А)}{-}=1$

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Совместные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же
испытании. В противном случае события называются несовместными.

Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус
вероятность их произведения:

$Р(А+В)=Р(А)+Р(В)-Р(А·В)$

В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.

Решение:

Обозначим события, пусть:

$А$ = кофе закончится в первом автомате,

$В$ = кофе закончится во втором автомате.

Тогда,

$A·B =$ кофе закончится в обоих автоматах,

$A + B =$ кофе закончится хотя бы в одном автомате.

По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.

События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий,
уменьшенной на вероятность их произведения:

$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$

Ответ: $0,88$

Теоретические основы математики

Элементы линейной и векторной алгебры

1. Матрицы
   1. Основные понятия о матрицах
   2. Действия над матрицами
2. Определители
   1. Определители второго порядка и их свойства
   2. Определители третьего порядка
   3. Определители n-го порядка
3. Обратная матрица
4. Системы линейных уравнений
   1. Основные понятия
   2. Формулы Крамера. Матричный способ решения систем линейных уравнений
   3. Решение систем линейных уравнений методом Гаусса
5. Элементы векторной алгебры
   1. Скалярные и векторные величины
   2. Линейные операции над векторами
   3. Угол между векторами. Проекция вектора на ось
   4. Линейная комбинация векторов. Базис
   5. Прямоугольная Декартова система координат
   6. Линейные операции над векторами, заданными в координатной форме
   7. Скалярное произведение векторов
   8. Векторное произведение векторов
   9. Смешанное произведение векторов

Учебно-методический комплекс составлен в соответствии с Государственным образовательным стандартом профессионального высшего образования РФ по дисциплине «Математика».